Valga como ejemplo el poema realizado entre toda la clase de 6º A (mediante la correspondiente dinámica grupal) sobre la función de nutrición:
viernes, 30 de octubre de 2015
POEMAS EN CIENCIAS NATURALES
Una estrategia interesante para trabajar la competencia lingüística, además de para asimilar contenidos propios de algún área, sería construir poemas relacionados con aquello que se está aprendiendo. El sentido de estos poemas no sería el estríctamente literario teniéndose en cuenta que, respecto a este bloque de lengua, se están iniciando.
Valga como ejemplo el poema realizado entre toda la clase de 6º A (mediante la correspondiente dinámica grupal) sobre la función de nutrición:
Podemos utilizar diferentes dinámicas de trabajo, pero resulta muy útil la de grupos en clase que vayan construyendo la poesía. Igualmente se podría ir conectando con lo aprendido en lengua sobre rimas, estrofas...
Valga como ejemplo el poema realizado entre toda la clase de 6º A (mediante la correspondiente dinámica grupal) sobre la función de nutrición:
martes, 9 de junio de 2015
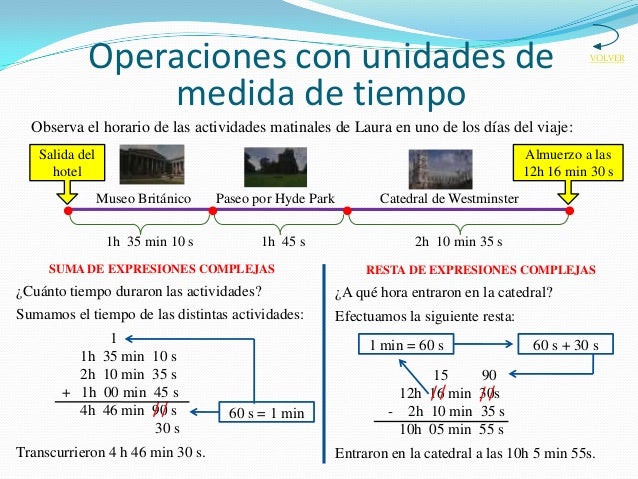
EL TIEMPO Y EL DINERO
En esta unidad vamos a trabajar los
siguientes contenidos:
- · SISTEMA SEXAGESIMAL: EXPRESIÓN COMPLEJA E INCOMPLEJA.
- · SUMA Y RESTA CON UNIDADES DE TIEMPO.
- · OPERACIONES CON EUROS Y DEVOLUCIONES.
- · REDONDEO EN LOS PRECIOS.
INTRODUCIÓN
¿Por qué una hora dura 60 minutos?
SISTEMA SEXAGESIMAL: EXPRESIÓN COMPLEJA E
INCOMPLEJA.
¿Cómo se pasar de expresión compleja a incompleja?
¿Cómo se pasar de expresión compleja a incompleja?
SUMA Y RESTA CON UNIDADES DE TIEMPO.
SUMA
RESTA
OPERACIONES CON EUROS Y
DEVOLUCIONES.
RECURSOS PARA PRACTICAR OPERACIONES CON EUROS
sábado, 30 de mayo de 2015
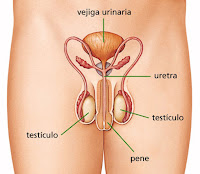
LA REPRODUCCIÓN
Esta entrada reúne información sobre la reproducción en todos sus tipos. No sigue la dinámica de otras entradas en cuanto a construcción de la unidad por parte del alumnado para Ciencias Naturales y Ciencias Sociales, y sí toda la información de manera directa.
REPRODUCCIÓN HUMANA
(Descargar esquema en PDF)
Sistema reproductor femenino
Sistema reproductor masculino
La fecundación
La fecundación humana
El embarazo semana a semana
El parto
La reproducción de las plantas
La reproducción de las plantas con flores
La reproducción sexual de las plantas
La reproducción asexual de las plantas
REPRODUCCIÓN HUMANA
(Descargar esquema en PDF)
Sistema reproductor femenino
Sistema reproductor masculino
La fecundación
La fecundación humana
El embarazo semana a semana
El parto
Fecundación y desarrollo embrionario
La ecografía
Etapas de la vida del ser humano
LA REPRODUCCIÓN DE LOS ANIMALES
Reproducción asexual en los animales
LA REPRODUCCIÓN DE LAS PLANTAS
La reproducción de las plantas con flores
La reproducción sexual de las plantas
La reproducción asexual de las plantas
La reproducción asexual de las plantas
La reproducción sexual de las plantas
miércoles, 22 de abril de 2015
PESO, LONGITUD Y SUPERFICIE
La unidad que vamos a trabajar trata de las unidades de longitud y sus cambios, unidades de peso y sus cambios, y las unidades de superficie.
Recordamos la relación entre unidades y los cambios de una a otra:
Y cómo se pueden diferenciar de forma compleja e incompleja:
Y ahora las unidades de superficie:
Cuando las unidades de superficie se utilizan para medir extensiones de campos, tierras, bosques, parcelas... utilizamos las Unidades agrarias:
Recordamos la relación entre unidades y los cambios de una a otra:
Y cómo se pueden diferenciar de forma compleja e incompleja:
Y ahora las unidades de superficie:
Observa que cada unidad de superficie equivale a 100 de la inmediatamente inferior:
Cuando las unidades de superficie se utilizan para medir extensiones de campos, tierras, bosques, parcelas... utilizamos las Unidades agrarias:
Utilizamos los siguientes RECURSOS:
Vídeo explicativo Unidades de Longitud
Vídeo explicativo unidades de Masa
Vídeo explicativo unidades de superficie
Actividades y explicaciones interactivas:
domingo, 19 de abril de 2015
LOS ANIMALES
Para esta unidad recomendamos visitar antes lo trabajado sobre SERES VIVOS anteriormente para así completar la información.
Por tanto, para construir esta unidad debemos tener en cuenta los siguientes apartados:
Vamos a trabajar siguiendo una adaptación de la metodología "Flipped Classroom" y para ello damos las ORIENTACIONES DE TRABAJO para construir la unidad:
Cada grupo expondrá su trabajo teniendo como referente de su AUTOEVALUACIÓN, la siguiente rúbrica de exposición oral:
Por tanto, para construir esta unidad debemos tener en cuenta los siguientes apartados:
Vamos a trabajar siguiendo una adaptación de la metodología "Flipped Classroom" y para ello damos las ORIENTACIONES DE TRABAJO para construir la unidad:
Cada grupo expondrá su trabajo teniendo como referente de su AUTOEVALUACIÓN, la siguiente rúbrica de exposición oral:
Proponemos las siguientes PÁGINAS CON INFORMACIÓN:
Los vertebrados
Anfibios y peces
Mamíferos
Invertebrados
Artrópodos
Aves y reptiles
Equinodermos
Moluscos
lunes, 6 de abril de 2015
PROPORCIONALIDAD Y PORCENTAJES
Hablamos de PROPORCIONALIDAD entre dos cantidades cuando al aumentar o disminuir una de ellas, la otra también lo hace de la misma manera.
Actividades y explicaciones
Sobre proporcionalidad
Proporcionalidad directa
Tablas de proporcionalidad
Situaciones de proporcionalidad
¿Qué haríamos si quisiéramos saber el precio de quince huevos si media docena cuesta 1,26? A esta operación la llamamos REDUCCIÓN A LA UNIDAD.
Actividades y explicaciones
Actividades y ejemplos de reducción a la unidad
A veces, para resolver problemas de proporcionalidad entre tres o más elementos (valores) conocidos y uno que no conocemos (incógnita), utilizamos la REGLA DE TRES. Sería hallar un cuarto valor o término, conociendo los otros tres.
Podríamos haber resuelto la situación reduciendo a la unidad, es decir, averiguando cuánto cuesta una bola y después multiplicando por 9, pero la regla en la práctica es más fácil al plantear problemas.
Vídeo: ¿Cómo resolver una regla de tres simple?
Actividades
Problemas para aplicar la regla de tres
Otro apartado importante de la unidad, y que seguro que ya conoces aunque no con este nombre (recuerda que has aprendido sobre fracciones o sobre decimales), son los PORCENTAJES.
Para CALCULAR EL PORCENTAJE aplicamos la misma operación que hacíamos para hallar la fracción de un número. Multiplicamos la cantidad por el número que indica el porcentaje (a modo de numerador) y luego dividimos entre 100 (a modo de denominador).
Explicación y práctica de porcentajes
Actividades de porcentajes y su relación con fracciones y decimales
Proporcionalidad y porcentajes
Fracciones decimales y porcentajes
Cálculo de porcentajes
Porcentajes, fracciones y decimales
Ahora, vamos a aplicar a situaciones cotidianas lo aprendido mediante estos Problemas
Seguimos...
Actividades y explicaciones
Sobre proporcionalidad
Proporcionalidad directa
Tablas de proporcionalidad
Situaciones de proporcionalidad
¿Qué haríamos si quisiéramos saber el precio de quince huevos si media docena cuesta 1,26? A esta operación la llamamos REDUCCIÓN A LA UNIDAD.
Actividades y explicaciones
Actividades y ejemplos de reducción a la unidad
A veces, para resolver problemas de proporcionalidad entre tres o más elementos (valores) conocidos y uno que no conocemos (incógnita), utilizamos la REGLA DE TRES. Sería hallar un cuarto valor o término, conociendo los otros tres.
Podríamos haber resuelto la situación reduciendo a la unidad, es decir, averiguando cuánto cuesta una bola y después multiplicando por 9, pero la regla en la práctica es más fácil al plantear problemas.
Vídeo: ¿Cómo resolver una regla de tres simple?
Actividades
Problemas para aplicar la regla de tres
Otro apartado importante de la unidad, y que seguro que ya conoces aunque no con este nombre (recuerda que has aprendido sobre fracciones o sobre decimales), son los PORCENTAJES.
 |
| Imagen de Vicens Vives |
 |
| Imagen de Vicens Vives |
Para CALCULAR EL PORCENTAJE aplicamos la misma operación que hacíamos para hallar la fracción de un número. Multiplicamos la cantidad por el número que indica el porcentaje (a modo de numerador) y luego dividimos entre 100 (a modo de denominador).
Explicación y práctica de porcentajes
Actividades de porcentajes y su relación con fracciones y decimales
Proporcionalidad y porcentajes
Fracciones decimales y porcentajes
Cálculo de porcentajes
Porcentajes, fracciones y decimales
Ahora, vamos a aplicar a situaciones cotidianas lo aprendido mediante estos Problemas
Seguimos...
jueves, 5 de marzo de 2015
OPERACIONES CON FRACCIONES
Una vez que hemos aprendido sobre fracciones, vamos a realizar operaciones con ellas.
En primer lugar, SUMAS Y RESTAS CON FRACCIONES DE IGUAL DENOMINADOR:
Para sumar o restar, se suman o restan los numeradores y se deja igual el denominador.
Actividades y explicaciones
Practica sumas y restas con igual denominador
Sumas y restas con igual denominador
Ahora vamos a multiplicar UN NÚMERO POR UNA FRACCIÓN y para ello se multiplica el número por el numerador y se deja el mismo denominador.
Actividades y explicaciones
Multiplicar número por fracción
Otra actividad de número por fracción
También podemos multiplicar fracción por fracción, el PRODUCTO DE FRACCIONES. Se halla multiplicando numerador por numerador y denominador por denominador.
Realmente, lo que estamos haciendo es averiguar la fracción de una fracción:
Actividades y explicaciones
Ejercicios con la multiplicación
Vamos a multiplicar fracciones
Explicaciones y actividades sobre el producto
Para DIVIDIR FRACCIONES, procedemos a multiplicar en cruz:
Actividades y explicaciones
División de fracciones
Vamos a dividir fracciones
Aumentamos la dificultad cuando vamos a SUMAR O RESTAR FRACCIONES DE DISTINTO DENOMINADOR. Para ello primero hay que reducir a común denominador:
Hallamos fracciones equivalentes a las dadas a partir del mcm de los denominadores. Después, ese número, se divide por el denominador y se multiplica por el numerador para obtener el nuevo numerador. Por último se procede a sumar o restar.
Actividades y explicaciones
Sumando y restando por pasos
Sumando con distinto denominador
Restando con distinto denominador
Operaciones con distinto denominador
La suma de fracciones
La resta de fracciones
Explicaciones sumas y restas
Vamos con la FRACCIÓN COMO DIVISIÓN DE NÚMEROS NATURALES. Esto se aplica cuando el numerador es múltiplo del denominador. Numerador es dividendo y denominador es divisor.
Pero si el numerador no es múltiplo del denominador, estamos ante una FRACCIÓN COMO DIVISIÓN DANDO COMO RESULTADO NÚMEROS DECIMALES.
No debemos olvidar lo que es una FRACCIÓN DECIMAL:
Así, relacionaríamos fracción con número decimal, con porcentaje y con fracción decimal:
Actividades
Escribe en forma de número decimal
Y terminamos con la FRACCIÓN DE UN NÚMERO. Es de las operaciones más funcionales ya que se trata de averiguar a qué cantidad exacta nos estamos refiriendo (3/4 de 25; 1/4 de 250...). Se halla multiplicando por el numerador y dividiendo por el denominador:
.jpg)
Actividades y explicaciones
Ejemplo de problema con fracción de un número
Problemas para resolver relacionados con la fracción de un número
Cálculo de fracción de un número
AUTOEVALUACIÓN FINAL
En primer lugar, SUMAS Y RESTAS CON FRACCIONES DE IGUAL DENOMINADOR:
Para sumar o restar, se suman o restan los numeradores y se deja igual el denominador.
Actividades y explicaciones
Practica sumas y restas con igual denominador
Sumas y restas con igual denominador
Ahora vamos a multiplicar UN NÚMERO POR UNA FRACCIÓN y para ello se multiplica el número por el numerador y se deja el mismo denominador.
Actividades y explicaciones
Multiplicar número por fracción
Otra actividad de número por fracción
También podemos multiplicar fracción por fracción, el PRODUCTO DE FRACCIONES. Se halla multiplicando numerador por numerador y denominador por denominador.
Actividades y explicaciones
Ejercicios con la multiplicación
Vamos a multiplicar fracciones
Explicaciones y actividades sobre el producto
Para DIVIDIR FRACCIONES, procedemos a multiplicar en cruz:
Actividades y explicaciones
División de fracciones
Vamos a dividir fracciones
Aumentamos la dificultad cuando vamos a SUMAR O RESTAR FRACCIONES DE DISTINTO DENOMINADOR. Para ello primero hay que reducir a común denominador:
Hallamos fracciones equivalentes a las dadas a partir del mcm de los denominadores. Después, ese número, se divide por el denominador y se multiplica por el numerador para obtener el nuevo numerador. Por último se procede a sumar o restar.
Actividades y explicaciones
Sumando y restando por pasos
Sumando con distinto denominador
Restando con distinto denominador
Operaciones con distinto denominador
La suma de fracciones
La resta de fracciones
Explicaciones sumas y restas
Vamos con la FRACCIÓN COMO DIVISIÓN DE NÚMEROS NATURALES. Esto se aplica cuando el numerador es múltiplo del denominador. Numerador es dividendo y denominador es divisor.
Pero si el numerador no es múltiplo del denominador, estamos ante una FRACCIÓN COMO DIVISIÓN DANDO COMO RESULTADO NÚMEROS DECIMALES.
No debemos olvidar lo que es una FRACCIÓN DECIMAL:
Así, relacionaríamos fracción con número decimal, con porcentaje y con fracción decimal:
Actividades
Escribe en forma de número decimal
Y terminamos con la FRACCIÓN DE UN NÚMERO. Es de las operaciones más funcionales ya que se trata de averiguar a qué cantidad exacta nos estamos refiriendo (3/4 de 25; 1/4 de 250...). Se halla multiplicando por el numerador y dividiendo por el denominador:
Actividades y explicaciones
Ejemplo de problema con fracción de un número
Problemas para resolver relacionados con la fracción de un número
Cálculo de fracción de un número
AUTOEVALUACIÓN FINAL
Suscribirse a:
Entradas (Atom)